Symmetric Key Encryption DES

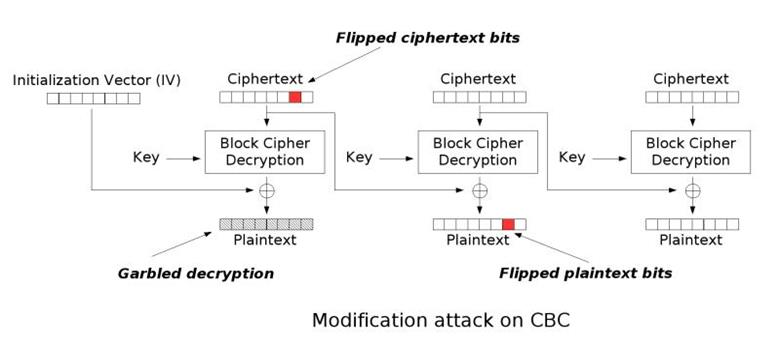
对称加密 (Symmetric Key Encryption)

对称加密是最快速、最简单的一种加密方式，加密（encryption）与解密（decryption）用的是同样的密钥（secret key）。对称加密有很多种算法，由于它效率很高，所以被广泛使用在很多加密协议的核心当中。自1977年美国颁布DES（Data Encryption Standard）密码算法作为美国数据加密标准以来，对称密码体制迅速发展，得到了世界各国的关注和普遍应用。对称密码体制从工作方式上可以分为分组加密和序列密码两大类。

对称加密算法的优点：算法公开、计算量小、加密速度快、加密效率高。

对称加密算法的缺点：交易双方都使用同样钥匙，安全性得不到保证。此外，每对用户每次使用对称加密算法时，都需要使用其他人不知道的惟一钥匙，这会使得发收信双方所拥有的钥匙数量呈几何级数增长，密钥管理成为用户的负担。对称加密算法在分布式网络系统上使用较为困难，主要是因为密钥管理困难，使用成本较高。而与公开密钥加密算法比起来，对称加密算法能够提供加密和认证却缺乏了签名功能，使得使用范围有所缩小。

对称加密通常使用的是相对较小的密钥，一般小于256 bit。因为密钥越大，加密越强，但加密与解密的过程越慢。

分组密码

分组密码：也叫块加密(block cyphers)，一次加密明文中的一个块。是将明文按一定的位长分组，明文组经过加密运算得到密文组，密文组经过解密运算（加密运算的逆运算），还原成明文组，有 ECB、CBC、CFB、OFB 四种工作模式。

序列密码

序列密码：也叫流加密(stream cyphers)，一次加密明文中的一个位。是指利用少量的密钥（制乱元素）通过某种复杂的运算（密码算法）产生大量的伪随机位流，用于对明文位流的加密。解密是指用同样的密钥和密码算法及与加密相同的伪随机位流，用以还原明文位流。

对称加密算法

常用对称加密算法包括 DES、3DES、AES

• DES（Data Encryption Standard）：数据加密标准，速度较快，适用于加密大量数据的场合。
• 3DES（Triple DES）：是基于DES，对一块数据用三个不同的密钥进行三次加密，强度更高。
• AES（Advanced Encryption Standard）：高级加密标准，是下一代的加密算法标准，速度快，安全级别高，支持128、192、256、512位密钥的加密。

算法特征

• 加密方和解密方使用同一个密钥。

• 加密解密的速度比较快，适合数据比较长时的使用。

• 密钥传输的过程不安全，且容易被破解，密钥管理也比较麻烦。

对称加密算法 Des

数据加密标准 Des

Des 设计理念

Des 设计中使用了分组密码设计的两个原则：混淆(confusion)和扩散(diffusion)，其目的是抗击敌手对密码系统的统计分析。混淆是使密文的统计特性与密钥的取值之间的关系 尽可能复杂化，以使密钥和明文以及密文之间的依赖性对密码分析者来说是无法利用的。扩散的作用就是将每一位明文的影响尽可能迅速地作用到较多的输出密文位中，以便在大量的 密文中消除明文的统计结构，并且使每一位密钥的影响尽可能迅速地扩展到较多的密文位中，以防对密钥进行逐段破译。

Des 加密算法结构流程

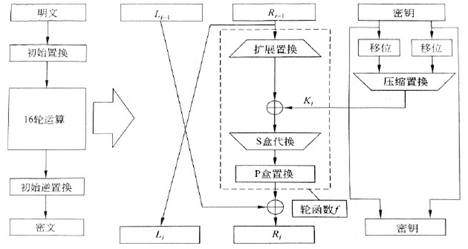
Des 加密算法电子编码本ECB模式流程

ECB 模式 & 性能

ECB 模式是最简单的加密模式，明文消息被分成固定大小的块（分组），并且每个块被单独加密。每个块的加密和解密都是独立的，且使用相同的方法进行加密，所以可以进行并行计算，但是这种方法一旦有一个块被破解，使用相同的方法可以解密所有的明文数据，安全性比较差。适用于数据较少的情形，加密前需要把明文数据填充到块大小的整倍数。

ECB算法优点：

简单、孤立，每个块单独运算。适合并行运算。传输错误一般只影响当前块。

ECB算法缺点：

同明文输出同密文，可能导致明文攻击。

ECB 加密 & 解密流程

• Encryption：

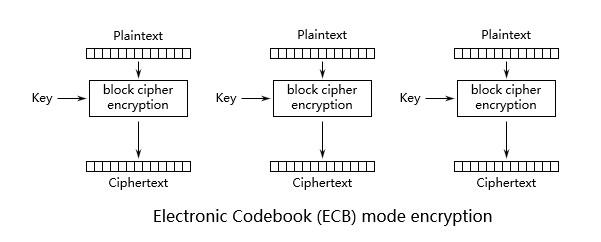
• Decryption：

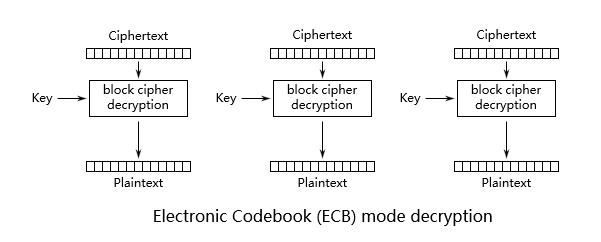
Des 分组加密所需参数

（1）Key：64位主密钥

（2）明文：64位的倍数

（3）密文：64位的倍数

（4）分组模式填充方式：PKCS5

（5）分组密码工作模式：EBC模式

Des 加密过程

（1）初始置换（IP）

根据初始置换表，对相应明文位置上的二进制进行置换操作，即把64 位的数据块的原第 58 位换到第一位，原第 50 位换到第二位.依此类推。目的在于打乱明文中各位的次序。

（2）子密钥生成

​

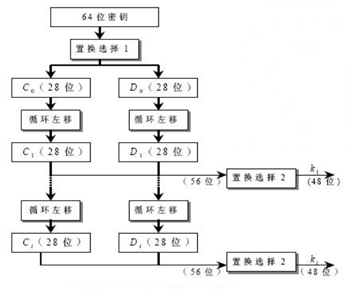
从用户处取得一个 64 位长的密钥key ，去除 64 位密钥中作为奇偶校验位的第 8、16、24、32、40、48、56、64 位，剩下的 56 位作为有效输入密钥。使用置换选择 1 对剩下的 56 位打乱，输出左 28 位 C 和右 28 位 D。两个部分都进行向左移位，移位后的两部分数据有两个作用。第一输出子密钥，每 i 轮两部分合在一起进行进行置换选择 2 得到迭代运算的第 i 个子密钥，第二作为下一轮子密钥运算。总共 16 轮运算（i=1,2,9,6 左移 1 位，其余 2 位）。

（3）16 轮迭代运算 (Des 核心)

​

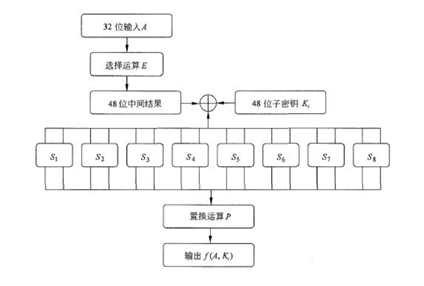
首先将二进制分为两个 32 位的部分：left 和 right。保持 left 不变，根据扩展置换表把 right 由 32 位扩展成 48 位。把扩展后的 48 位 right 与第 i 次迭代生成的 48 位子密钥按位异或运算，形成一个新的 48 位的 right。然后与主密钥生成的 48 位子密钥异或操作，然后进行 S 盒代换，得到一个 32 位的二进制数据，将数据进行 P 盒置换后，与 left 进行异或操作，结果作为下一轮迭代运算的 right 部分。上一轮 right 部分作为下一轮运算的 left 部分。第 16 次迭代不交换两者的数值。

（4）初始逆置换

16轮迭代运算后，依据初始逆置换表，对相应位置的二进制数进行置换操作。最后得到密文。

Des 解密过程

Des 算法是对称的，既可用加密又可用于解密，只不过在16次迭代中使用的密钥次序正好相反。解密时，第一次迭代使用子密钥K16，依次类推。

分组密码工作方式

ECB，将明文消息分成 n 个 m bit 组(m 通常为 64)，如果长度不是 m 整数倍，则在明文末尾进行填充 (本次实验采用PKCS5)

对称加密算法 Des 实现

语言 & 环境

（1）语言

Python

（2）环境

Python版本：python 3.7

Python工具：PyCharm Professional

操作流程

（1）在 < text.txt > 文件中读取需要加密的文本

（2）在 < key.txt > 文件中写入随机产生固定长度的Key

（3）在 < ciphertext.txt > 文件中写入DES加密、Base64编码后的数据

（4）在 < plaintext.txt > 文件中写入Base64解码、DES解密后的数据

主要代码

（1）Main 函数

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
 1     if __name__ == '__main__':
 2         key = getRandomString()
 3         with open('text.txt', 'r+') as fr:
 4             text = (fr.read())          # 从 'text.txt' 文件中读取加密文本
 5         D = Des()
 6         C = (base64.b64encode((D.encrypt(key, text, True)).encode("utf8"))).decode()  # 加密
 7         C1 = (base64.b64decode(C)).decode()
 8         P = D.decrypt(key, C1, True)                # 解密
 9         with open('key.txt', 'w+') as fwk:          # 存储密钥
10             fwk.write(key)
11         with open('ciphertext.txt', 'w+') as fwc:   # 存储密文
12             fwc.write(C)
13         with open('plaintext.txt', 'w+') as fwp:    # 存储明文
14             fwp.writelines(P)
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（2）Encryption

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def encrypt(self, key, text, padding):          # DES 加密函数
2         return self.run(key, text, ENCRYPT, padding)
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（3）Decryption

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def decrypt(self, key, text, padding):          # DES 解密函数
2         return self.run(key, text, DECRYPT, padding)
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < <

（4）字符串和比特数组之间相互转换

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
 1     def string_to_bit_array(text):             # 字符串-->bit数组
 2         array = list()
 3         for char in text:
 4             binval = binvalue(char, 8)         # 获得每个字符的二进制
 5             array.extend([int(x) for x in list(binval)])
 6         return array
 7 
 8     def bit_array_to_string(array):            # bit数组-->字符串
 9         res = ''.join([chr(int(y, 2)) for y in [''.join([str(x) for x in bytes]) for bytes in nsplit(array, 8)]])
10         return res
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < <

（5）二进制处理

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def binvalue(val, bitsize):              # 以给定大小的字符返回二进制值
2         binval = bin(val)[2:] if isinstance(val, int) else bin(ord(val))[2:]
3         if len(binval) > bitsize:
4             raise Exception("binary value larger than the expected size")
5         while len(binval) < bitsize:
6             binval = "0" + binval
7         return binval
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < <

（6）列表划分

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def nsplit(s, n):                     # 将列表拆分为大小为'n'的子列表
2         return [s[k:k + n] for k in range(0, len(s), n)]
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（7）获取随机固定长度序列 Key

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def getRandomString(slen=8):        # 获得key的随机序列
2         return ''.join(random.sample(string.ascii_letters + string.digits, slen))
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（8）初始化 Des 类

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def __init__(self):
2         self.password = None            # 存放初始key
3         self.text = None                # 存放明文
4         self.keys = list()              # 存放key值列表集合
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（9）PKCS5 模式 数据填充

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def addPadding(self):  # PKCS5 进行数据填充,不管是否是BlockSize的整数倍都需要进行填充
2         pad_len = 8 - (len(self.text) % 8)
3         self.text += pad_len * chr(pad_len)
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（10）数据填充移除

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def removePadding(self, data):                     # 删除纯文本的填充
2         pad_len = ord(data[-1])
3         return data[:-pad_len]
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（11）获取 Key 值集合列表

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
1     def generatekeys(self):                       # 统计计算所有key值的算法
2         self.keys = []
3         key = string_to_bit_array(self.password)
4         key = self.permut(key, CP_1)              # 置换选择1 初始化key 64bit-->56bit
5         g, d = nsplit(key, 28)                    # 分片 (g->LEFT),(d->RIGHT)
6         for i in range(16):                       # 16轮循环
7             g, d = self.shift(g, d, SHIFT[i])       # (g->LEFT),(d->RIGHT)分别进行移位操作
8             tmp = g + d                             # 合并 28bit+28bit-->56bit
9             self.keys.append(self.permut(tmp, CP_2))     # 置换选择2 56bit-->48bit
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（12）Key 值移位函数

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def shift(self, g, d, n):                     # 每轮key值产生所需的函数
2         return g[n:] + g[:n], d[n:] + d[:n]
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（13）基本置换 扩展置换 压缩置换

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def permut(self, block, table):              # 置换(本程序中充当基本置换、压缩置换的角色)
2         return [block[x - 1] for x in table]
3 
4     def expand(self, block, table):              # 扩展置换
5         return [block[x - 1] for x in table]
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（14）自定义 XOR 函数

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
1     def xor(self, t1, t2):                      # 应用xor并返回结果列表
2         return [x ^ y for x, y in zip(t1, t2)]
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

（15）S 盒代换

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
 1     def substitute(self, d_e):                           # S盒代换
 2         subblocks = nsplit(d_e, 6)                       # 将位数组分割为6位的子列表
 3         result = list()
 4         for i in range(len(subblocks)):                  # 遍历子列表
 5             block = subblocks[i]
 6             row = int(str(block[0]) + str(block[5]), 2)  # 得到第一位和最后一个位表示的行
 7             column = int(''.join([str(x) for x in block[1:][:-1]]), 2) #得到第二、三、四、五位表示的列
 8             val = S_BOX[i][row][column]                # 取为本轮分配的SBOX[i]中的值
 9             bin = binvalue(val, 4)                     # 将值转换为二进制
10             result += [int(x) for x in bin]            # 将二进制值添加到结果列表中
11         return result
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < <

（16）16轮运算核心

> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
 1     for block in text_blocks:               # 遍历所有数据块
 2         block = string_to_bit_array(block)
 3         block = self.permut(block, IP)      # 数据块的初始置换
 4         g, d = nsplit(block, 32)            # 数据块分片 g(LEFT), d(RIGHT)
 5         tmp = None
 6         for i in range(16):                 # 16轮循环
 7             d_e = self.expand(d, E)         # d(RIGHT)的扩展 32bit-->48bit
 8             if action == ENCRYPT:
 9                 tmp = self.xor(self.keys[i], d_e)
10             else:
11                 tmp = self.xor(self.keys[15 - i], d_e)  # 如果是解密的话先使用最后的key
12             tmp = self.substitute(tmp)                  # S盒代换 48bit-->32bit
13             tmp = self.permut(tmp, P)                   # P盒置换
14             tmp = self.xor(g, tmp)
15             g = d
16             d = tmp
17         result += self.permut(d + g, IP_1)              # 数据块的初始逆置换
18     final_res = bit_array_to_string(result)
< < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < < 

数据测试

（1）测试结果

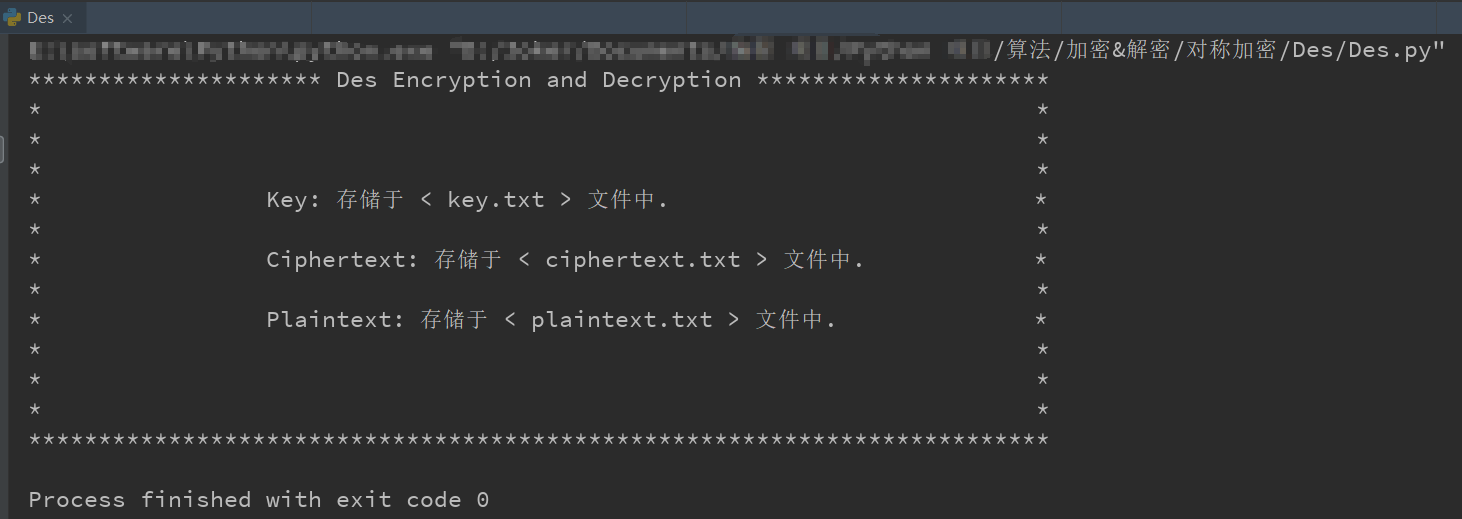
（2）在 < text.txt > 文件中读取需要加密的文本

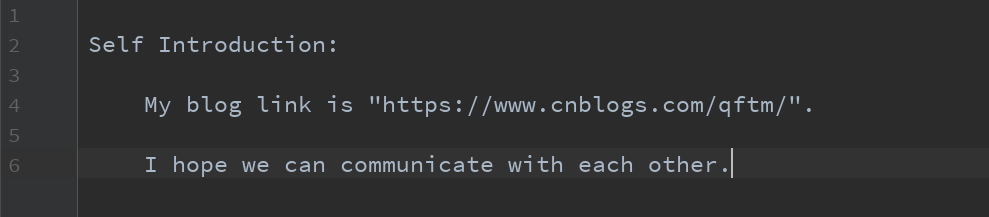
（3）在 < key.txt > 文件中写入随机产生固定长度的Key

（4）在 < ciphertext.txt > 文件中写入DES加密、Base64编码后的数据

（5）在 < plaintext.txt > 文件中写入Base64解码、DES解密后的数据

项目地址

项目地址

https://github.com/Qftm/Symmetric_Key_Encryption_DES