C Programming Language Data Structure Learning

C 数据结构
编程开发
Publish Date:   2018-11-25
Update Date:   2020-08-16
Word Count:   5.2k
Read Times:   24 Min

C语言实现二叉树的创建&遍历

算法思想

重点是递归的使用

利用扩展先序遍历序列创建二叉链表。

采用类似先序遍历的递归算法，首先读入当前根结点的数据，如果是’.’则将当前树根置为空，否则申请一个新结点，存入当前根结点的数据，分别用当前根结点的左子域和右子域进行递归调用，创建左、右子树。

代码实现

#include <stdio.h>
#include <stdlib.h>

typedef char DataType;             //二叉链表结点的数据类型 

typedef struct Node               //定义二叉树的二叉链表结点结构 
{
    DataType data;
    struct Node *LChild;         //左子树 
    struct Node *RChild;         //右子树     
}BiTNode,*BiTree;

void CreateBiTree(BiTree *bt);   //创建二叉链表函数 
void PreOrder(BiTree root);      //先序遍历二叉树
void InOrder(BiTree root);       //中序遍历二叉树
void PostOrder(BiTree root);     //后序遍历二叉树

int main()
{
    BiTree bt;
    int choice;
    while(true)
    {                   //二叉树操作选择菜单 
    printf("*****************Please enter your choice*****************\n\n");
    printf("                choice 1：创建二叉树\n");
        printf("                choice 2：先序遍历二叉树\n");
        printf("                choice 3：中序遍历二叉树\n");
        printf("                choice 4：后序遍历二叉树\n");
        printf("                choice 0：退出\n\n");
        scanf("%d",&choice);
        switch(choice)
        {
            case 1: CreateBiTree(&bt);
                    break;
            case 2: PreOrder(bt);             
                      printf("\n");
                       break;

            case 3: InOrder(bt);               
                    printf("\n");
                       break;
            case 4: PostOrder(bt);                
                    printf("\n");
                       break;
            case 0: exit(0);                
                    break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }        
    }
    return 0; 
} 

void CreateBiTree(BiTree *bt)
{
    char ch;
    printf("Please enter data:");
    getchar();
    ch = getchar();
    if(ch == '.')              //读入的数据是'.'则将当前树根置为空 
    {
        *bt = NULL;
    }
    else                      //读入正常数据,为当前树根分配地址空间 
    {
        *bt = (BiTree)malloc(sizeof(BiTNode));
        (*bt)->data = ch;
        CreateBiTree(&((*bt)->LChild)); //递归调用CreateBiTree()函数,处理左子树 
        CreateBiTree(&((*bt)->RChild)); //递归调用CreateBiTree()函数,处理右子树 
    }
}

void PreOrder(BiTree root) //先序遍历二叉树,root为指向二叉树根结点的指针 
{
    if(root!=NULL)    
    {
        printf("%c ",root->data);      //访问根结点 
        PreOrder(root->LChild);        //先序遍历左子树 
        PreOrder(root->RChild);        //先序遍历右子树
    }
}

void InOrder(BiTree root)    //中序遍历二叉树,root为指向二叉树根结点的指针
{ 
    if(root!=NULL)    
    {
        InOrder(root->LChild);      //中序遍历左子树
        printf("%c ",root->data);      //访问根结点 
        InOrder(root->RChild);      //中序遍历右子树
    }
}

void PostOrder(BiTree root)     //中序遍历二叉树,root为指向二叉树根结点的指针
{ 
    if(root!=NULL)             
    {
        PostOrder(root->LChild);      //后序遍历左子树
        PostOrder(root->RChild);      //后序遍历右子树
        printf("%c ",root->data);      //访问根结点 
    }
}

C语言实现二叉树中统计叶子结点的个数&度为1&度为2的结点个数

算法思想

统计二叉树中叶子结点的个数和度为1、度为2的结点个数，因此可以参照二叉树三种遍历算法（先序、中序、后序）中的任何一种去完成，只需将访问操作具体变为判断是否为叶子结点和度为1、度为2的结点及统计操作即可。

代码实现

#include <stdio.h>
#include <stdlib.h>

int LeafCount=0;
int Degree1Count=0;
int Degree2Count=0;

typedef char DataType;             //二叉链表结点的数据类型 

typedef struct Node               //定义二叉树的二叉链表结点结构 
{
    DataType data;
    struct Node *LChild;         //左子树 
    struct Node *RChild;         //右子树     
}BiTNode,*BiTree;

void CreateBiTree(BiTree *bt);   //创建二叉链表函数 
void PreOrder(BiTree root);      //先序遍历二叉树
void InOrder(BiTree root);       //中序遍历二叉树
void PostOrder(BiTree root);     //后序遍历二叉树
void Leaf(BiTree root);          //统计叶子结点数目 
void Degree1(BiTree root);        //统计度为1的结点数目
void Degree2(BiTree root);        //统计度为2的结点数目

int main()
{
    BiTree bt;
    int choice;
    while(true)
    {                   //二叉树操作选择菜单 
    printf("*****************Please enter your choice*****************\n\n");
    printf("                choice 1：创建二叉树\n");
        printf("                choice 2：先序遍历二叉树\n");
        printf("                choice 3：中序遍历二叉树\n");
        printf("                choice 4：后序遍历二叉树\n");
        printf("                choice 5：打印叶子结点数目\n");
        printf("                choice 6：打印度为1的结点数目\n");
        printf("                choice 7：打印度为2的结点数目\n");
        printf("                choice 0：退出\n\n");
        scanf("%d",&choice);
        switch(choice)
        {
            case 1: CreateBiTree(&bt);
                    break;
            case 2: PreOrder(bt);             
                      printf("\n");
                       break;

            case 3: InOrder(bt);               
                    printf("\n");
                       break;
            case 4: PostOrder(bt);                
                    printf("\n");
                       break;
            case 5: Leaf(bt);             
                      printf("该二叉树叶子结点的数目为：%d\n",LeafCount);
                       break;
            case 6: Degree1(bt);               
                    printf("该二叉树度为1的结点数目为：%d\n",Degree1Count);
                       break;
            case 7: Degree2(bt);                
                    printf("该二叉树度为2的结点数目为：%d\n",Degree2Count);
                       break;
            case 0: exit(0);                
                    break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }        
    }
    return 0; 
} 

void CreateBiTree(BiTree *bt)
{
    char ch;
    printf("Please enter data:");
    getchar();
    ch = getchar();
    if(ch == '.')              //读入的数据是'.'则将当前树根置为空 
    {
        *bt = NULL;
    }
    else                      //读入正常数据,为当前树根分配地址空间 
    {
        *bt = (BiTree)malloc(sizeof(BiTNode));
        (*bt)->data = ch;
        CreateBiTree(&((*bt)->LChild)); //递归调用CreateBiTree()函数,处理左子树 
        CreateBiTree(&((*bt)->RChild)); //递归调用CreateBiTree()函数,处理右子树 
    }
}

void PreOrder(BiTree root) //先序遍历二叉树,root为指向二叉树根结点的指针 
{
    if(root!=NULL)    
    {
        printf("%c ",root->data);      //访问根结点 
        PreOrder(root->LChild);        //先序遍历左子树 
        PreOrder(root->RChild);        //先序遍历右子树
    }
}

void InOrder(BiTree root)    //中序遍历二叉树,root为指向二叉树根结点的指针
{ 
    if(root!=NULL)    
    {
        InOrder(root->LChild);      //中序遍历左子树
        printf("%c ",root->data);      //访问根结点 
        InOrder(root->RChild);      //中序遍历右子树
    }
}

void PostOrder(BiTree root)     //中序遍历二叉树,root为指向二叉树根结点的指针
{ 
    if(root!=NULL)             
    {
        PostOrder(root->LChild);      //后序遍历左子树
        PostOrder(root->RChild);      //后序遍历右子树
        printf("%c ",root->data);      //访问根结点 
    }
}

void Leaf(BiTree root)
{
    if(root!=NULL)
    {
        Leaf(root->LChild);
        Leaf(root->RChild);
        if(root->LChild==NULL && root->RChild==NULL)
        {
            LeafCount++;   //统计叶子结点数目
        }
    }
} 

void Degree1(BiTree root)
{
    if(root!=NULL)
    {
        Degree1(root->LChild);
        Degree1(root->RChild);
        if((root->LChild==NULL && root->RChild!=NULL)||(root->LChild!=NULL && root->RChild==NULL))
        {
            Degree1Count++;   //统计度为1的结点数目
        }
    }
} 

void Degree2(BiTree root)
{
    if(root!=NULL)
    {
        Degree2(root->LChild);
        Degree2(root->RChild);
        if(root->LChild!=NULL && root->RChild!=NULL)
        {
            Degree2Count++;   //统计度为2的结点数目
        }
    }
}

C语言实现循环队列的初始化&进队&出队&读取队头元素&判空

队列是另一种限定性的线性表，它只允许在表的一端插入元素，而在另一端删除元素，所以队列具有先进先出的特性。

算法思想

系统用到的抽象数据类型定义

ADT Queue{

  数据元素：可以是任意类型的数据，但必须属于同一个数据对象。

  数据关系：队列中数据元素之间是线性关系。

  基本操作：
    1. initQueue(&Q)；       //循环队列初始化
    2. enterQueue(&Q);      //循环队列入队操作
    3. deleteQueue(&Q);     //循环队列出队操作
    4. isEmpty(&Q);         //判断队列是否为空
    5. getHead(&Q,&x);      //读取队列的队头元素 ,指针x指向队头元素

}ADT Queue;

系统中子程序及功能要求

  • void initQueue(SeqQueue *Q);

操作前提：Q为未初始化的队列。

操作结果：将Q初始化为一个空队列。

  • int enterQueue(SeqQueue *Q,int n);

操作前提：队列Q已存在。

操作结果：在队列Q的队尾插入n。操作成功，返回值为True，否则返回值为False。

  • void deleteQueue(SeqQueue *Q);

操作前提：队列Q已存在。

操作结果：将队列Q的队头元素出队。操作成功，返回值为True，否则返回值为False。

  • int isEmpty(SeqQueue *Q);

操作前提：队列Q已存在。

操作结果：若队列为空，则返回True,否则返回False。

  • int getHead(SeqQueue *Q,int *x);

操作前提：队列Q已存在。

操作结果：取队列Q的队头元素（该元素不出队），并用x带回其值。操作成功，返回值为True，否则返回值为False。

代码实现-1

/*顺序表实现循环队列的基本操作 (损失一个数组空间)*/ 

#include
#include 

#define Queue_Size 50           //队列的最大长度 
#define True 1
#define False 0

typedef struct
{          
    int elem[Queue_Size];       //队列的元素空间 
    int front;                  //头指针指示器 
    int rear;                    //尾指针指示器 
}SeqQueue;

void initQueue(SeqQueue *Q);        //循环队列初始化 
int enterQueue(SeqQueue *Q,int n);  //循环队列入队操作 
void deleteQueue(SeqQueue *Q);      //循环队列出队操作 
int isEmpty(SeqQueue *Q);           //判断队列是否为空 
int getHead(SeqQueue *Q,int *x);   //读取队列的队头元素 ,指针x指向队头元素 

int main()
{
    SeqQueue Q;
    int choice,x;
    while(true)           //循环队列操作选择菜单 
    {
        printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Queue initialization\n");
        printf("                choice 2：Into the queue\n");
        printf("                choice 3：Out of the queue\n");
        printf("                choice 4：Determine whether the queue is empty\n");
        printf("                choice 5：Get queue head\n");
        printf("                choice 0：exit\n\n");
        scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                initQueue(&Q);
                break;
            case 2:
                int n;
                printf("Please enter the number into the queue elements：");
                scanf("%d",&n);     //读入存入的队列元素个数 
                                              //三目运算符根据返回值判断元素是否进队成功 
                (enterQueue(&Q,n)==1)?printf("%d个元素依次进队成功\n",n):printf("%d个元素依次进队失败\n",n);    
                break;
            case 3:
                deleteQueue(&Q);
                break;
            case 4:            //三目运算符根据返回值判断队列是否为空 
                (isEmpty(&Q)==1)?printf("An empty Queue\n"):printf("Not an empty Queue\n");
                break;
            case 5:              //三目运算符根据返回值判断队头元素是否读取成功  
                (getHead(&Q,&x)==False)?printf("An empty Queue error!!!!\n"):printf("Get head successful，队头元素为：%d\n",x); 
                 break; 
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
}

void initQueue(SeqQueue *Q)
{   //将 *Q 初始化为一个空的循环队列 
    Q->front=Q->rear=0;
}

int enterQueue(SeqQueue *Q,int n)
{  //将元素n入队 
    int n1,n2;    
    printf("Please enter into the queue elements in turn:\n");  
    for(n1=0;n1rear+1)%Queue_Size==Q->front) return False;   //尾指针加1追上头指针，标志队列已经满了 
        scanf("%d",&n2);        
        Q->elem[Q->rear]=n2;      //元素进队 
        Q->rear=(Q->rear+1)%Queue_Size;                 //重新设置队尾指针                  
    }
    return True;          //操作成功 
}

void deleteQueue(SeqQueue *Q)
{   //删除队列的队头元素 
    int a;
    if(Q->front==Q->rear)
    {               //队列为空，删除失败 
        printf("An empty Queue error!!!!\n");  
    }
    else
    {
        a=Q->elem[Q->front];           //删除前先读取队头元素 
        Q->front=(Q->front+1)%Queue_Size;   //重新设置队头指针 
        printf("队顶元素%d出队成功.\n",a);    //操作成功 
    }  
}

int isEmpty(SeqQueue *Q)
{
    if(Q->front==Q->rear)
    {               //判断队列为空,返回True 
        return True;  
    }
    return False;  //否则返回False 
}

int getHead(SeqQueue *Q,int *x)
{
    if(Q->front==Q->rear)
    {               //队列为空，读取失败 
        return False;
    }
    else
    {
        *x=Q->elem[Q->front];  //操作成功 
        return True;            
    }  
}

代码实现-2

/*顺序表实现队列的一系列操作（设置flag标志不损失数组空间）*/ 

#include
#include

#define Queue_Size 50     //队列的最大长度 
#define OK 1
#define ERROR 0

typedef struct
{
    int elem[Queue_Size];       //队列的元素空间 
    int front;                  //头指针指示器 
    int rear;                    //尾指针指示器 
    int flag;                    //flag，判断队列是否为空的标志 
}SeqQueue;

/**********************各个子函数的定义*********************/
void initQueue(SeqQueue *Q);        //循环队列初始化 
int enterQueue(SeqQueue *Q,int n);  //循环队列入队操作 
void deleteQueue(SeqQueue *Q);      //循环队列出队操作 
int isEmpty(SeqQueue *Q);           //判断队列是否为空 
int getHead(SeqQueue *Q,int *x);   //读取队列的队头元素 ,指针x指向队头元素 

int main(){
    SeqQueue Q;
    int choice;
    while(true)          //循环队列操作选择菜单 
    {
        printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Queue initialization\n");
        printf("                choice 2：Into the queue\n");
        printf("                choice 3：Out of the queue\n");
        printf("                choice 4：Determine whether the queue is empty\n");
        printf("                choice 5：Get queue head\n");
        printf("                choice 0：exit\n\n");
         scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                initQueue(&Q);
                break;
            case 2:
                int n;
                printf("Please enter the number into the queue elements：");
                scanf("%d",&n);  //读入存入的队列元素个数 
                                //三目运算符根据返回值判断元素是否进队成功 
                (enterQueue(&Q,n)==1)?printf("%d个元素依次进队成功\n",n):printf("%d个元素依次进队失败\n",n);    
                break;
            case 3:
                deleteQueue(&Q);
                break;
            case 4:            //三目运算符根据返回值判断队列是否为空 
                (isEmpty(&Q)==1)?printf("An empty Queue\n"):printf("Not an empty Queue\n");
                break;
            case 5:              //三目运算符根据返回值判断队头元素是否读取成功  
                int x;
                (getHead(&Q,&x)==0)?printf("An empty Queue error!!!!\n"):printf("Get head successful，队头元素为：%d\n",x); 
                 break;     
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
}

/**********************各个子函数功能的实现*********************/
void initQueue(SeqQueue *Q)   
{                            //将 *Q 初始化为一个空的循环队列 
    Q->front=Q->rear=0;
    Q->flag=0;
}
int enterQueue(SeqQueue *Q,int n)  //进队列 
{    //将元素n入队
    int n1,n2;
    if((Q->front==Q->rear)&&(Q->flag==1)) return ERROR;   //标志队列已经满了 
    printf("Please enter into the queue elements in turn:\n");  
    for(n1=0;n1elem[Q->rear]=n2;
        Q->rear=(Q->rear+1)%Queue_Size;                 //重新设置队尾指针
        if(Q->front==Q->rear)        //此处有两种情况：1.元素没有全部进入队列，空间已经满了 2.元素全部进入队列，空间刚刚好好 
        {
            Q->flag=1;       //flag=1:队列空间存满 
            return ERROR; 
        }                 
    }
    return OK;
} 
void deleteQueue(SeqQueue *Q)
{                               //删除队列的队头元素 
    int a;
    if((Q->front==Q->rear)&&(Q->flag==0))        //队列为空，删除失败 
    {
        printf("An empty Queue error!!!!\n");
    }
    else
    {
        a=Q->elem[Q->front];               //删除前先读取队头元素 
        Q->front=(Q->front+1)%Queue_Size;  //重新设置队头指针 
        printf("队顶元素%d出队成功.\n",a); //操作成功
        if(Q->front==Q->rear) Q->flag=0;   //flag=0:队列中的元素全部出队 
    }  
}

int isEmpty(SeqQueue *Q)
{
    if((Q->front==Q->rear)&&(Q->flag==0))
    {               //判断队列为空,返回OK
        return OK;  
    }
    return ERROR;  //否则返回ERROR 
}

int getHead(SeqQueue *Q,int *x)
{
    if((Q->front==Q->rear)&&(Q->flag==0))
    {               //队列为空，读取失败 
        return ERROR;
    }
    else
    {
        *x=Q->elem[Q->front];  //操作成功 
        return OK;            
    }  
}

C语言实现顺序栈的初始化&进栈&出栈&读取栈顶元素

代码实现

/*顺序表实现栈的一系列操作*/ 

#include
#include 

#define Stack_Size 50             //设栈中元素个数为50 
#define OK 1
#define ERROR 0

typedef struct                
{
    int elem[Stack_Size];          //用来存放栈中元素的一维数组 
    int top;                       //用来存放栈顶元素的下标，top为 -1 表示空栈 
}SeqStack;

/**********************各个子函数的定义*********************/
int initStack(SeqStack *S);         //初始化顺序栈 
void push(SeqStack *S,int n);          //顺序栈进栈运算 
void pop(SeqStack *S);                //顺序栈出栈运算 
int getTop(SeqStack *S,int *s);     //读取栈顶元素 

int main()
{
    SeqStack *S;
    int choice;
    while(true)
    {
        printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Stack initialization\n");
        printf("                choice 2：Into the stack\n");
        printf("                choice 3：Out of the stack\n");
        printf("                choice 4：Read the stack elements\n");
        printf("                choice 0：exit\n\n");
         scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                (initStack(S)==1)?printf("initStck success.\n"):printf("initStack ERROR\n");
                break;
            case 2:
                int n;
                printf("Please enter the number into the stack elements：");
                scanf("%d",&n);
                push(S,n);
                break;
            case 3:
                pop(S);
                break;
            case 4:
                int* s;
                (getTop(S,s)==1)? printf("栈顶元素是：%d.\n",*s):printf("An empty stack error!!!!\n"); //三目运算符
                break;        
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
} 

/**********************各个子函数功能的实现*********************/
int initStack(SeqStack *S)    //初始化顺序栈 
{         
    if(S!=NULL)
    {
        S->top=-1;             //置为空栈 
        return OK;
    }
    else return ERROR;        //内存空间不足 
}
void push(SeqStack *S,int n)  //进栈 ，将元素压入栈中 
{   
    int n1,n2;
    if(((S->top)+n)<=Stack_Size-1)   //压入栈中的元素不能超过栈的最大存储 
    {  
        printf("Please enter into the stack elements in turn:\n");  
        for(n1=0;n1top++;                    //移动栈顶指针 
            S->elem[S->top]=n2;
        }
        printf("%d个元素依次进栈成功\n",n);
    }
    else
    {                    //栈空间不够 
        printf("ERROR There is insufficient space on the stack.\n");            
    }                 
}
void pop(SeqStack *S)
{     //栈顶元素出栈 
    int a;
    if(S->top==-1)
    {               //栈为空，操作失败 
        printf("An empty stack error!!!!\n");
    }
    else
    {
        a=S->elem[S->top];
        S->top--;
        printf("栈顶元素%d出栈成功.\n",a);  //出栈成功 
    }  

}
int getTop(SeqStack *S,int *s)   //获取栈顶元素 
{    
    if(S->top==-1)
    {               //栈为空，操作失败 
        return ERROR;
    }
    else
    {
        *s=S->elem[S->top];   //读取栈顶元素成功 
        return OK;
    }
}

C语言实现链栈的初始化&进栈&出栈&读取栈顶元素

代码实现

/*链表实现栈的一系列操作*/

#include
#include 

#define OK 1
#define ERROR 0

typedef struct node
{
    int data;
    struct node *next;
}LinkStackNode,*LinkStack;

/**********************各个子函数的定义*********************/
void initStack(LinkStack *top);       //初始化链栈 
int push(LinkStack top,int n);        //链栈进栈操作 
void pop(LinkStack top);              //链栈出栈操作 
int getTop(LinkStack top,int *s);     //读取链栈栈顶元素 

int main()
{
    LinkStack top;
    int choice;
    while(true)
    {
        printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Stack initialization\n");
        printf("                choice 2：Into the stack\n");
        printf("                choice 3：Out of the stack\n");
        printf("                choice 4：Read the stack elements\n");
        printf("                choice 0：exit\n\n");
         scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                initStack(&top);
                break;
            case 2:
                int n;
                printf("Please enter the number into the stack elements：");
                scanf("%d",&n);
                (push(top,n)==1)?printf("%d个元素依次进栈成功\n",n):printf("%d个元素依次进栈失败\n",n);    
                break;
            case 3:
                pop(top);
                break;
            case 4:
                int* s;
                (getTop(top,s)==1)? printf("栈顶元素是：%d.\n",*s):printf("An empty stack error!!!!\n"); //三目运算符
                break;        
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
}

/**********************各个子函数功能的实现*********************/
void initStack(LinkStack *top)
{   //初始化 
    *top=(LinkStack)malloc(sizeof(LinkStackNode));  //带头结点的单链表 
    (*top)->next=NULL; 
} 

int push(LinkStack top,int n)    //进栈 ，将元素压入栈中 
{        
    LinkStackNode *temp;
    int n1,n2;
    printf("Please enter into the stack elements in turn:\n");  
    for(n1=0;n1data=n2;
        temp->next=top->next;          //采用头插法存储元素 
        top->next=temp; 
    }
    return OK;
}

void pop(LinkStack top)          //栈顶元素出栈 
{           
    int a;
    LinkStackNode *temp;
    if(top->next==NULL)
    {               //栈为空，出栈失败 
        printf("An empty stack error!!!!\n");
    }
    else
    {
        temp=top->next;
        a=temp->data;
        top->next=temp->next;
        free(temp);
        printf("栈顶元素%d出栈成功.\n",a);  
    }  
}

int getTop(LinkStack top,int *s)        //获读取栈顶元素 
{    
    if(top->next==NULL)              //栈为空，读取栈顶元素失败 
    { 
        return ERROR;
    }
    else
    {
        *s=(top->next)->data;           //读取栈顶元素，不出栈 
        return OK;
    }
}

C语言实现链队列的初始化&进队&出队

代码实现

/*链表实现队列的一系列操作*/ 

#include
#include 

#define OK 1
#define ERROR 0

typedef struct node
{
    int data;                            //数据域 
    struct node *next;                  //指针域 
}LinkQueueNode;
typedef struct
{
    LinkQueueNode *front;              //头指针 
    LinkQueueNode *rear;               //尾指针 
}LinkQueue;

/**********************各个子函数的定义*********************/
void initQueue(LinkQueue *Q);          //链队列初始化       
int enterQueue(LinkQueue *Q,int n);    //链队列入队操作 
void deleteQueue(LinkQueue *Q);        //链队列出队操作 

int main()
{
    LinkQueue Q;
    int choice;
    while(true)
    {
        printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Queue initialization\n");
        printf("                choice 2：Into the queue\n");
        printf("                choice 3：Out of the queue\n");
        printf("                choice 0：exit\n\n");
         scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                initQueue(&Q);
                break;
            case 2:
                int n;
                printf("Please enter the number into the queue elements：");
                scanf("%d",&n);
                (enterQueue(&Q,n)==1)?printf("%d个元素依次进队成功\n",n):printf("%d个元素依次进队失败\n",n);    
                break;
            case 3:
                deleteQueue(&Q);
                break;    
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
}

/**********************各个子函数功能的实现*********************/
void initQueue(LinkQueue *Q)   
{            //将 Q 初始化为一个空链队列 
    Q->front=(LinkQueueNode *)malloc(sizeof(LinkQueueNode));
    Q->rear=Q->front;
    Q->front->next=NULL;
}

int enterQueue(LinkQueue *Q,int n)  //进队列 
{
    LinkQueueNode *temp;
    int n1,n2;
    printf("Please enter into the queue elements in turn:\n");  
    for(n1=0;n1data=n2;
        temp->next=NULL;
        Q->rear->next=temp; 
        Q->rear=temp;                 //队尾指针后移                    
    }
    return OK;
}

void deleteQueue(LinkQueue *Q)
{
    int a;
    LinkQueueNode *temp;
    if(Q->front==Q->rear)               //队为空，出栈失败 
    {
        printf("An empty Queue error!!!!\n");
    }
    else
    {
        temp=Q->front->next;
        a=temp->data;
        Q->front->next=temp->next;
        if(Q->front==temp)           //如果队中只有一个元素X，则X出队后成为空队 
        {
            Q->rear=Q->front;
        }
        free(temp);                            //释放存储空间 
        printf("队顶元素%d出队成功.\n",a);   
    }  
}

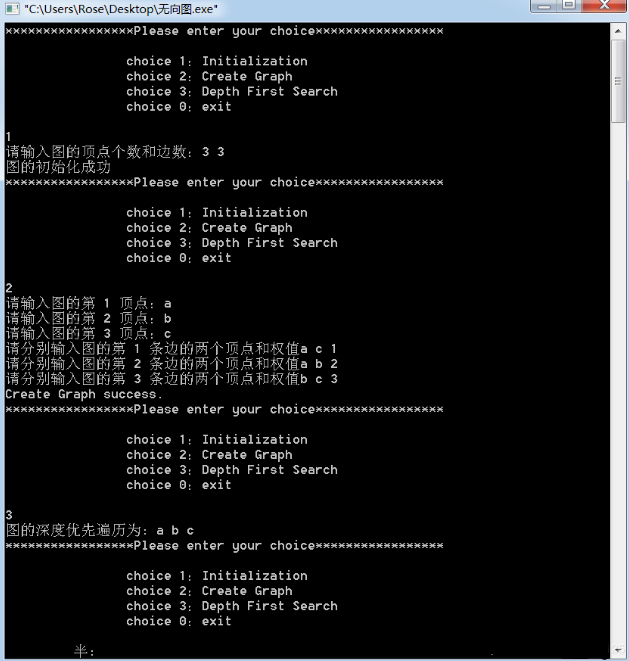
C语言实现邻接矩阵创建无向图

代码实现

/* '邻接矩阵' 实现无向图的创建、深度优先遍历*/
#include 
#include  

#define MaxVex      100          //最多顶点个数
#define INFINITY    32768        //表示极大值，即 ∞
#define TRUE        1
#define FALSE       0
#define OK          1
#define ERROR       0

typedef char VertexType;    //假设顶点数据类型为字符类型
typedef int  EdgeType;      //对于无权图，用1或0表示是否相邻，对带权图，则为权值类型 
typedef struct
{
    VertexType vertex[MaxVex];            //顶点数组
    EdgeType arcs[MaxVex][MaxVex];       //邻接矩阵
    int    vexnum,arcnum;                //图中的顶点数和边数 
}Graph;

int visited[MaxVex];    //访问标志数组    

/**********************各个子函数的定义*********************/
void init(Graph *G);                    //初始化邻接矩阵 
int LocateVertex(Graph *G,VertexType v);//求顶点位置函数
int createUDG(Graph *G);                //创建一个无向图 
void DepthFirstSearch(Graph G, int i);  //图的深度优先遍历
void TraverseGraph(Graph G);

/**************************主函数*************************/
int main()
{
    Graph G;
    int choice;
    while(true)
    {
         printf("*****************Please enter your choice*****************\n\n");
        printf("                choice 1：Initialization\n");
        printf("                choice 2：Create Graph\n");
                printf("                choice 3：Depth First Search\n");       
        printf("                choice 0：exit\n\n");
         scanf("%d",&choice);
        switch(choice)
        {
            case 1:
                init(&G);
                break;
            case 2:
                (createUDG(&G)==1)?printf("Create Graph success.\n"):printf("Create Graph ERROR\n");
                break;
            case 3:
                printf("图的深度优先遍历为: ");
                TraverseGraph(G);
                break;        
            case 0:
                exit(0);
                break;
            default:
                printf("ERROR！！\n");
                exit(0);
                break;
        }
    }
    return 0;
} 

/**********************各个子函数功能的实现*********************/
void init(Graph *G)   //初始化邻接矩阵 
{
    int i,j;
    printf("请输入图的顶点个数和边数："); 
    scanf("%d %d",&(G->vexnum),&(G->arcnum));//输入图的顶点个数和边数 
    for(i=0;ivexnum;i++)              //初始化
    {
        for(j=0;jvexnum;j++)
        {
            G->arcs[i][j]=INFINITY;
        }
    } 
    printf("图的初始化成功\n"); 
}

int LocateVertex(Graph *G,VertexType v)  //查找并返回顶点的位置 
{
    int j=0,k;
    for(k=0;kvexnum;k++)
    {
        if(G->vertex[k]==v)
        {
            j=k;
            break;
        }
    }
    return j;    
}

int createUDG(Graph *G)  //创建一个无向图
{
    int i,j,k,weight;
    VertexType v1,v2;
    for(i=0;ivexnum;i++)
    {
        printf("请输入图的第 %d 顶点：",i+1);
        getchar();
        scanf("%c",&(G->vertex[i]));     //输入图的顶点集 
    } 
    for(k=0;karcnum;k++)
    {
        printf("请分别输入图的第 %d 条边的两个顶点和权值",k+1);
        getchar();
        scanf("%c %c %d",&v1,&v2,&weight);//输入一条边的两个顶点、权值 
        i=LocateVertex(G,v1);
        j=LocateVertex(G,v2);
        G->arcs[i][j]=weight;     //建立顶点之间的关系 
        G->arcs[j][i]=weight;
    } 
    return OK;
}

void DepthFirstSearch(Graph G, int i)   //图的深度优先遍历
{
    int j;
    visited[i] = TRUE;
    printf("%c ",G.vertex[i]);  
    for (j=0; j

代码测试

image-20200408001227139

Author: Qftm
Link: http://Qftm.github.io/2018/11/25/CDateStructLearning/
Reprint policy: All articles in this blog are used except for special statements CC BY 4.0 reprint polocy. If reproduced, please indicate source Qftm !
C 数据结构
 Previous
NNctf2018 Web WriteUp NNctf2018 Web WriteUp
WEB1.超简单分值：100 类型：WEB 已解决 题目：超简单的web题 http://gxnnctf.gxsosec.cn:12311/ ) 代码审计 <?php $white_list = range(0,9); require
2018-12-22 CTF
CTF
Next 
CSRF 漏洞分析与测试 CSRF 漏洞分析与测试
CSRF简介CSRF中文名：跨站请求伪造，英文译为：Cross-site request forgery，CSRF攻击就是attacker（攻击者）利用victim（受害者）尚未失效的身份认证信息(cookie、session等)，以某种方
2018-11-07 Web安全
CSRF DVWA
  TOC